二叉树的遍历

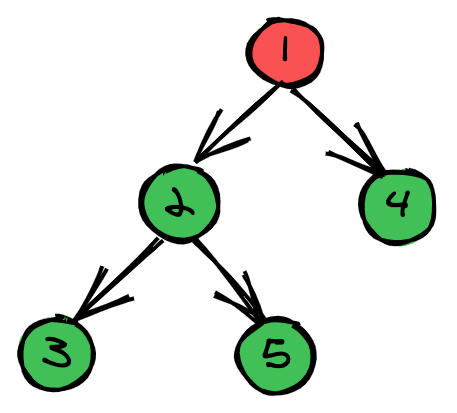
对于线性数据结构（Array、Linked List、Queues、Stacks等），一般只能通过一种逻辑方式来进行遍历，但是树比较不同，我们可以用不同的方式遍历：

binary_tree
  • 深度优先
    • 先序遍历: 1, 2, 3, 5, 4
    • 中序遍历: 3, 2, 5, 1, 4
    • 后序遍历: 3, 5, 2, 4, 1
  • 广度优先（层序遍历）: 1, 2, 4, 3, 5

这篇文章主要关注深度优先遍历的部分，对于每种遍历，我们都可以采用递归和迭代（非递归）的方式。

首先我们定义一下Tree中的Node类

1
2
3
4
5
6
7
8
9

class Node {
    int key;
    Node left, right;

    public Node(int item) {
        key = item;
        left = right = null;
    }
}

先序遍历

递归方式

思路

1
2
3
4

1 − 访问根节点
2 − 递归遍历左子树
3 − 递归遍历右子树
直到访问所有节点

代码

1
2
3
4
5
6
7
8

void recursivePreorder(Node node) 
{ 
    if (node == null) return; 

    System.out.print(node.key + " "); 
    recursivePreorder(node.left); 
    recursivePreorder(node.right); 
}

非递归方式

思路

我们知道在计算机系统中，递归其实是在调用栈的基础上实现的，为了将一个递归过程转换为迭代过程，我们需要显式维护一个栈。以下是基于栈的先序遍历迭代过程：

1
2
3
4
5
6
7

1 - 创建一个空栈nodeStack，并将根节点入栈
2 - 在nodeStack不为空的情况下执行以下操作
    a - 从堆栈中弹出一个节点并打印出来
    b - 将弹出节点的右子节点入栈
    c - 将弹出节点的左子节点入栈

（右子节点在左子节点之前入栈，以确保左子树先被处理）

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

void iterativePreorder(Node root) {
    if (root == null) return;

    Stack<Node> nodeStack = new Stack<Node>();
    nodeStack.push(root);

    while (!nodeStack.empty()) {
        Node current = nodeStack.pop();
        System.out.print(current.key + " ");

        if (current.right != null) nodeStack.push(current.right);
        if (current.left != null) nodeStack.push(current.left);
    }
}

中序遍历

递归方式

思路

1
2
3
4

1 − 递归遍历左子树
2 − 访问根节点
3 − 递归遍历右子树
直到访问所有节点

代码

1
2
3
4
5
6
7
8

void recursiveInorder(Node node) 
{ 
    if (node == null) return; 

    recursiveInorder(node.left); 
    System.out.print(node.key + " "); 
    recursiveInorder(node.right); 
}

非递归方式

思路

1
2
3
4
5
6
7
8

1 - 创建一个空栈nodeStack和一个Node变量current
    并将current初始化为根节点（直接用root亦可，此处只是为了命名清晰）
2 - 将current入栈，设置current = current.left，直到current为null
3 - 如果current为null，且堆栈不是空的，则
    a - 从堆栈中弹出最上面的节点popped_node
    b - 打印弹出的节点，设置current = popped_node.right
    c - 重复步骤2
4 - 直到current为null，且栈为空，结束

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

void iterativeInorder(Node root) { 
    if (root == null) return; 

    Stack<Node> nodeStack = new Stack<Node>(); 
    Node current = root; 

    while (current != null || !nodeStack.empty()) { 
        if (current !=  null) { 
            nodeStack.push(current); 
            current = current.left; 
        } else {
            current = nodeStack.pop(); 
            System.out.print(current.key + " "); 
            current = current.right; 
        }
    } 
}

后序遍历

递归方式

思路

1
2
3
4

1 − 递归遍历左子树
2 − 递归遍历右子树
3 − 访问根节点
直到访问所有节点

代码

1
2
3
4
5
6
7
8

void recursivePostorder(Node node) 
{ 
    if (node == null) return; 

    recursivePostorder(node.left); 
    recursivePostorder(node.right); 
    System.out.print(node.key + " "); 
}

非递归方式(使用一个栈)

后序遍历的非递归实现比上边两个遍历复杂一点，同时方法也比较多，我们逐个来看。

思路1

思路1是的中心思想是： 和中序遍历一样，先左指针向下移动到最左边的节点，不同的是我们需要一个标记位pre用来记忆上一次打印（访问）的节点。
当我们到达最左边的节点时，如果它没有右子节点或者右子节点等于pre，说明右子树已经遍历完了，打印它。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

1 - 创建一个空栈nodeStack和一个Node变量current，并将current初始化为根节点
2 - 执行以下操作直到current为null
    a - 将current入栈
    b - 设置current = current.left
3 - 将current设置为栈顶元素
    a - 如果 current.right等于null或者pre，意味着我们已经遍历了右边的子树，则：
        - 打印curren，并将其出栈
        - 令 pre=current; current=null（这样我们就不会再往下看左边的孩子了）
    b - 否则令 current=current.right（先遍历右子树）
4 - 直到current为null，且栈为空，结束

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

void iterativePostorder1(Node root) { 
    if (root == null) return; 

    Stack<Node> nodeStack = new Stack<Node>(); 
    Node current = root, pre = null;

    while (current != null || !nodeStack.empty()) {
        if (current != null) {
            nodeStack.push(current);
            current = current.left;
        } else {
            current = nodeStack.peek();
            if (current.right == null || current.right == pre) {
                System.out.print(current.key + " ");
                nodeStack.pop();
                pre = current;
                current = null;
            } else {
                current = current.right;
            }
        }
    }
}

思路2

有了思路1的基础，我们来看看它的变体：
在向左遍历的时候，直接将current节点入栈两次。
在弹出的时候如果发现stack.peek()和current一样，那么就继续current.right，否则就打印current。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

void iterativePostorder2(Node root) { 
    if (root == null) return; 

    Stack<Node> nodeStack = new Stack<Node>(); 
    Node current = root;

    while (true) {
        if (current != null) {
            nodeStack.push(current);
            nodeStack.push(current);
            current = current.left;
        } else if (nodeStack.empty()) {
            return;
        } else {
            current = nodeStack.pop();
            if (!nodeStack.empty() && current == nodeStack.peek()) {
                current = current.right;
            } else {
                System.out.print(current.key + " ");
                current = null;
            }
        }
    }
}

非递归方式(使用两个栈)

对于后序遍历的非递归方式，我们也可以用两个栈，这个方法有点类似于非递归的先序遍历，但有两点主要区别：

  1. 不打印节点，而是把它push到另一个堆栈里
  2. 先入栈左子节点，后入栈右子节点

思路

1
2
3
4
5

1 - 将根节点push到第一个堆栈
2 - 在第一个堆栈不为空时进行循环：
    a - 从第一个堆栈中弹出一个节点，并将其push到第二堆栈中
    b - 将弹出的节点的左右子节点push到第一个堆栈中
3 - 打印第二个堆栈的内容

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

void iterativePostorder3(Node root) { 
    if (root == null) return; 

    Stack<Node> nodeStack1 = new Stack<Node>(); 
    Stack<Node> nodeStack2 = new Stack<Node>(); 

    nodeStack1.push(root);

    while (!nodeStack1.empty()) {
        Node current = nodeStack.pop();
        nodeStack2.push(current);
        
        if (current.left != null) nodeStack1.push(current.left);
        if (current.right != null) nodeStack1.push(current.right);
    }

    while (!nodeStack2.empty()) { 
        Node temp = nodeStack2.pop(); 
        System.out.print(temp.key + " "); 
    } 
}

总结

二叉树的遍历很有趣也很有用，它既简单又复杂，简单在于思路上，复杂在于多变和细节上，其实二叉树的遍历还有其他的方法，以后有机会再补充。
从上边的描述中可以看出，非递归过程其实和递归过程的本质其实没什么区别，只不过对于非递归，我们需要自己维护一个堆栈来模拟操作系统里的递归函数调用栈。