blog-applicative-02

在函数式编程基础[一]–范畴论和Functor 中，我们了解了什么是Category和Functors，现在我们继续往下看Applicative Functor。

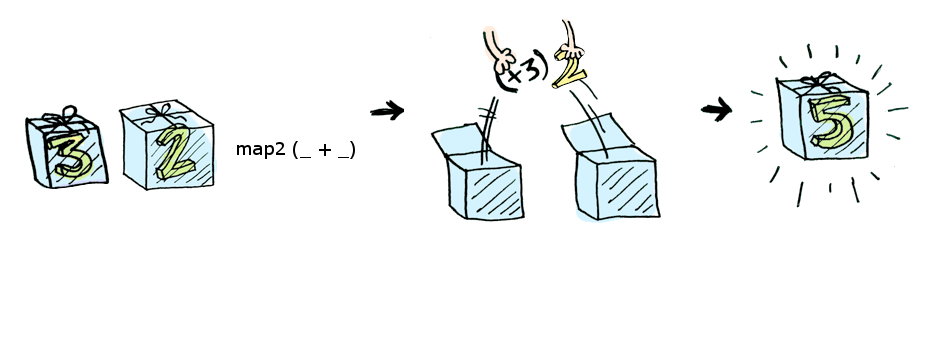
先快速回顾一下Functor，我们知道Maybe Functor可以帮我们实现下面的运算：

1
2
3

-- fmap :: (Int -> Int) -> Maybe Int -> Maybe Int
fmap negate (Just 2) -- Just (-2)
fmap negate Nothing  -- Nothing

但是我们如何计算两个Maybe值的和呢？比如 Just(3) + Just(2). 这就是Applicative要帮我们解决的问题。

Applicative 定义

Applicative由三部分组成：

  • 一个类型构造函数f –例如 List、Maybe
  • 一个函数pure : a -> f a，其中a可以是任何类型(包括函数类型)
  • 一个函数apply(<*>) : f (a -> b) -> f a -> f b，其中a和b可以是任何类型(包括函数类型)

具体定义如下：

1
2
3

class (Functor f) => Applicative f where
    pure  :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

pure

本质上，pure函数是一个构造函数，可以将任何类型a的值转换为f a的值，pure将其参数 “提升(lifts)/注入(inject) “到类型构造函数所定义的相应类型中(例如从Int到List Int)。我们来看看Maybe的实现：

1
2
3
4

instance Applicative Maybe where
    pure                  = Just
    (Just f) <*> (Just x) = Just (f x)
    _        <*> _        = Nothing

这里pure就是把值用Just包起来：

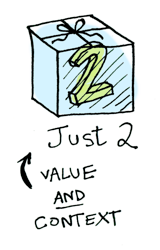
value_and_context

因为a可以是任意类型，我们当然也可以包一个函数：

function_and_context

顺便看一下List的实现：

1
2
3

instance Applicative [] where  
    pure x = [x]  
    fs <*> xs = [f x | f <- fs, x <- xs]

apply(<*>)

Apply函数接收一个嵌入到类型构造函数定义的上下文中的函数(如 Maybe(a -> b))，并将其提升/转换为类型构造函数领域中的函数(Maybe a → Maybe b)。

回到最开始那个问题：如何计算两个Maybe值的，我们可以利用apply方法：

1

Just (+3) <*> Just(2) == Just 5
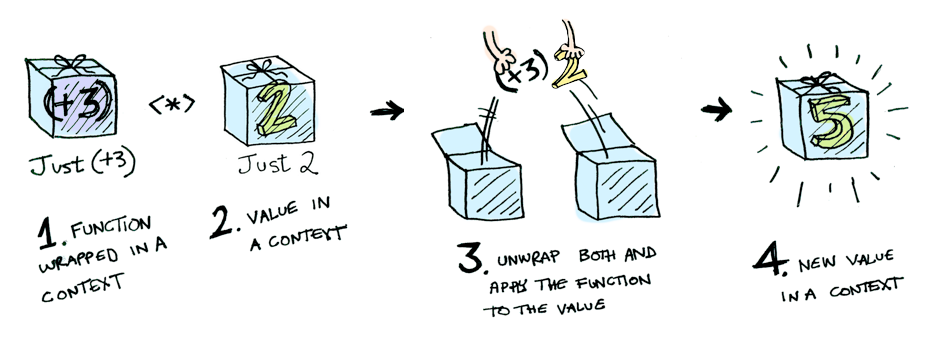
applicative_just

apply函数接收一个单个参数的函数(a -> b)，如果我们给它传一个多参数的方法会怎么样呢？

a1 -> a2 -> ... -> an

如果我们把这个函数f传给pure，会得到一个被f封装的多参数方法：f (a1 -> a2 -> ... -> an)。

再将它传给apply就可以得到：

f a1 -> f (a2 -> ... -> an)

我们可以重复使用apply函数将其转换为f a1 -> f a2 -> ... -> f an。

我们可以通过这种方式将多参数的函数提升到Applicative中，如图：

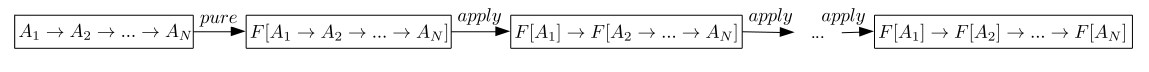
applicativefunctor1
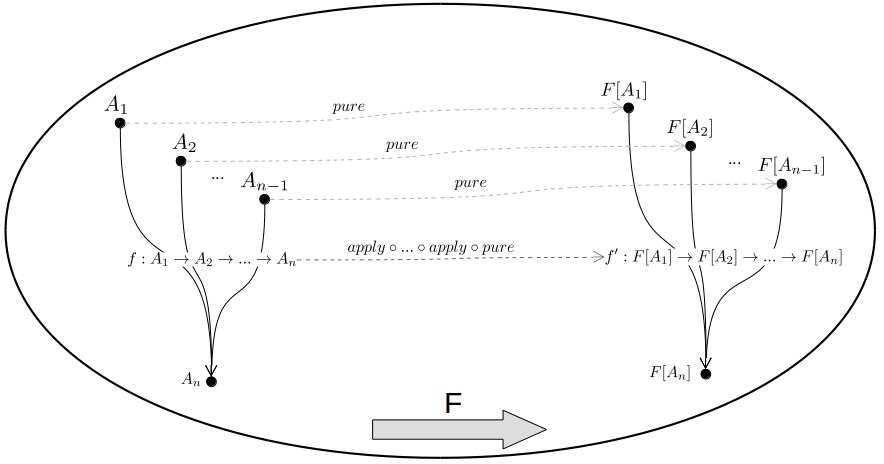
applicativefunctorhask

我们用一个两个参数的函数举例：(+) :: Num a => a -> a -> a

1

(pure(+) <*> Just(2)) <*> Just(4) -- Just 6

Applicative Laws

和Functor一样，Applicative也需要满足一些laws：

1
2
3
4

pure id <*> v = v                            -- Identity
pure f <*> pure x = pure (f x)               -- Homomorphism
u <*> pure y = pure ($ y) <*> u              -- Interchange
pure (.) <*> u <*> v <*> w = u <*> (v <*> w) -- Composition

这里非常有趣，我们怎么实现才能满足这些laws呢？一般是选择最普通，最平常，最没有特色，最直观的方式实现pure函数。比如对于List Applicative，pure是这样实现的：

1

pure x = [x]

我们当然可以实现成 [x, x]，但是就可能会不符合某些laws了。

Conclusion

当我们看到Applicative的时候，可以联想到context，wrapper，box这些概念。我们将某些数据封装到盒子中，然后将针对盒子中具体数据的函数也打包到盒子里，两个盒子相互作用，从而得到一个带有新值的新盒子。

References