函数式编程基础--范畴论和Functor

Martin Kuppe曾经绘制了一幅数学的景观图，在这幅图中，数学的分支分布在大陆的各个地方。在这其中有一个高高悬浮的月亮，它提供了一望无际的地形，使我们能够看到各个领域之间的关系，这些关系在地面上可能是无法察觉的，这证明数学中看似不相关的领域其实也不是那么不同。而这个强大的月亮就是Category Theory(范畴论)。

比如Functor、Applicative和Monad这些概念最初就是在Category Theory中定义的，它们现在已经成为函数式编程（FP）语言和范式中的重要组成部分了。虽然理解这些概念在FP领域的意义和应用并不需要对相应数学定义和公理有非常深入的认识。但是，这些基础理论和常识可以帮助FP程序员理解常用库和工具的设计和结构，提高工作效率。也就是说我们在平常的编码中可能不会应用到很深的概念，但是他们被广泛地应用在各种开源库中。我们先来了解Category(范畴)和Functor(函子)是什么东西。

范畴

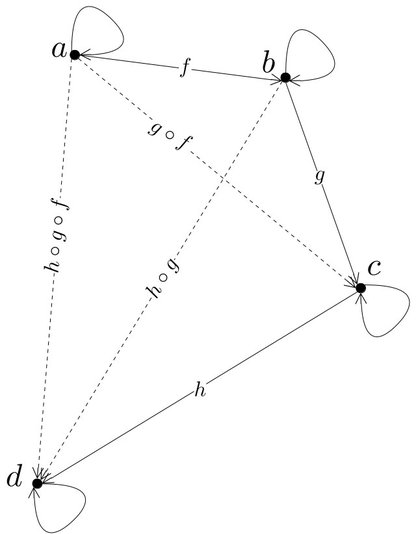
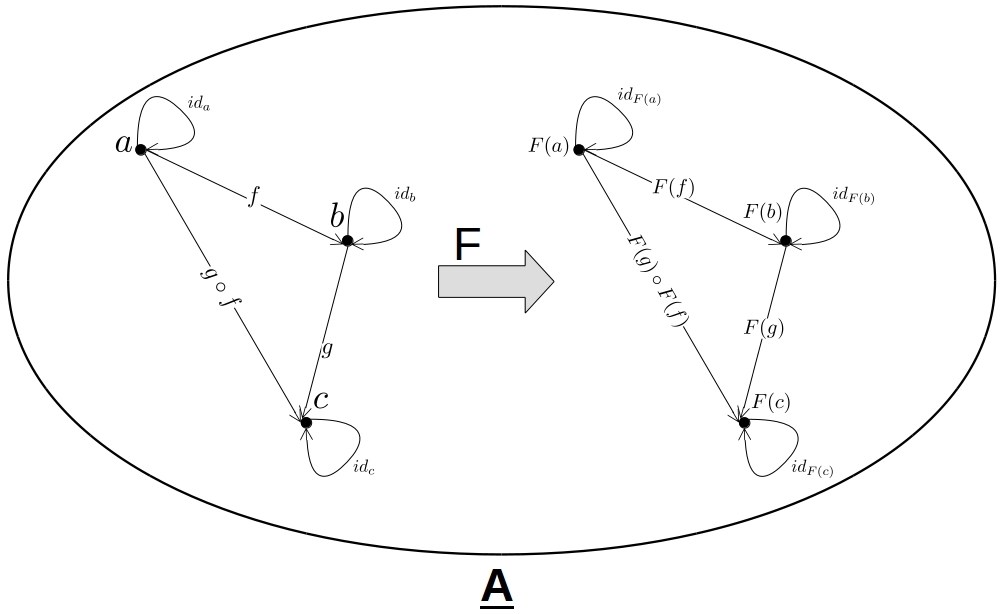
一个Category(范畴)是一个包含了对象及对象之间关系(箭头)的代数结构。比如一个Category C，它由一些对象 ob(C) 和连接这些对象的箭头(态射) hom(C) 组成。换句话说，每个箭头f都可以用它所连接的一对对象 [a,b] 来定义，我们将其写作f : a → b。

Category中的箭头是可以组合的，对于每一个f : a→b和g : b→c，它们的组合g ∘ f也是一个箭头，它连接a和c，即g ∘ f : a→c。(g ∘ f 可以读作g after f，也就是先apply f，再apply g)

并不是说有了对象和箭头就是一个Category，他们需要满足下列的条件：

箭头间的组合需要满足结合律，也就是说，对于每三个箭头:
h ∘ (g ∘ f) = (h ∘ g) ∘ f
对于每一个对象a，都有一个连接其自身的箭头(identity arrow)
ia : a→a
即对于任一个 f : a→b，都有: ib ∘ f = f = f ∘ ia

用一个图来直观的表示Category：

实际例子

OOP

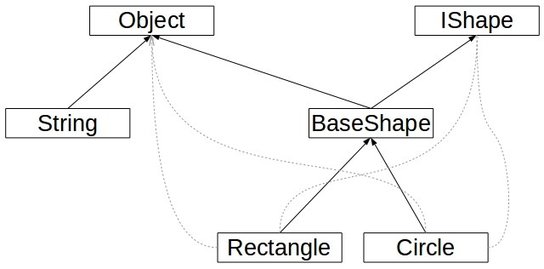
用我们熟悉的面向对象来举个例子，在面向对象编程中，类的层次结构也形成了Category。Category中的对象a是类型（如类、特征和接口）。如果A是B的子类型，我们就将类型A和B用一个箭头连接。这些箭头是可以组合的，因为如果A是B的子类型，B是C的子类型，那么A就是C的子类型。这里identity就代表每个类型都是自己的子类型，如下图。

The Hask Category

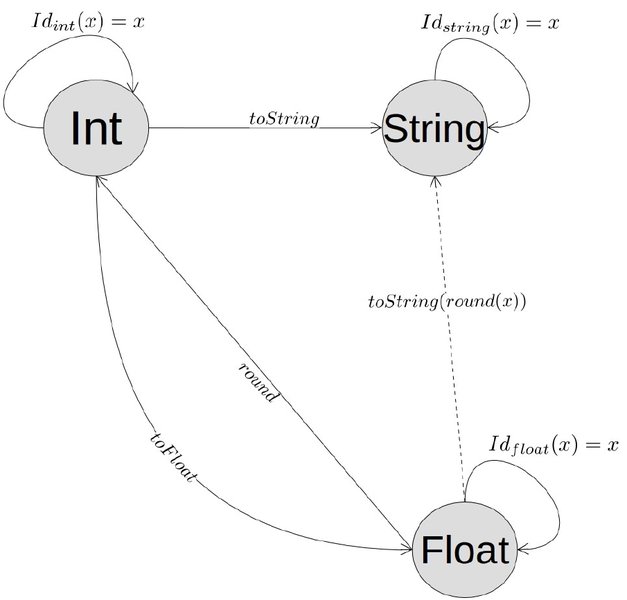
说完面向对象，也得说说函数式编程。在函数式编程中有一个特殊的Category：Hask。Haskell编程语言的类型就是Hask中的对象–即Ob(Hask)={Int，String，…}。我们也可以将其推广到其他语言的类型比如Scala。在Haskell中我们有从a类型到b类型的方法，在Hask中对应的就是两种类型之间的一个箭头，箭头的组合其实就是函数的组合。identity箭头对应的是identity函数，下图描述了Hask Category的一部分。

Functor

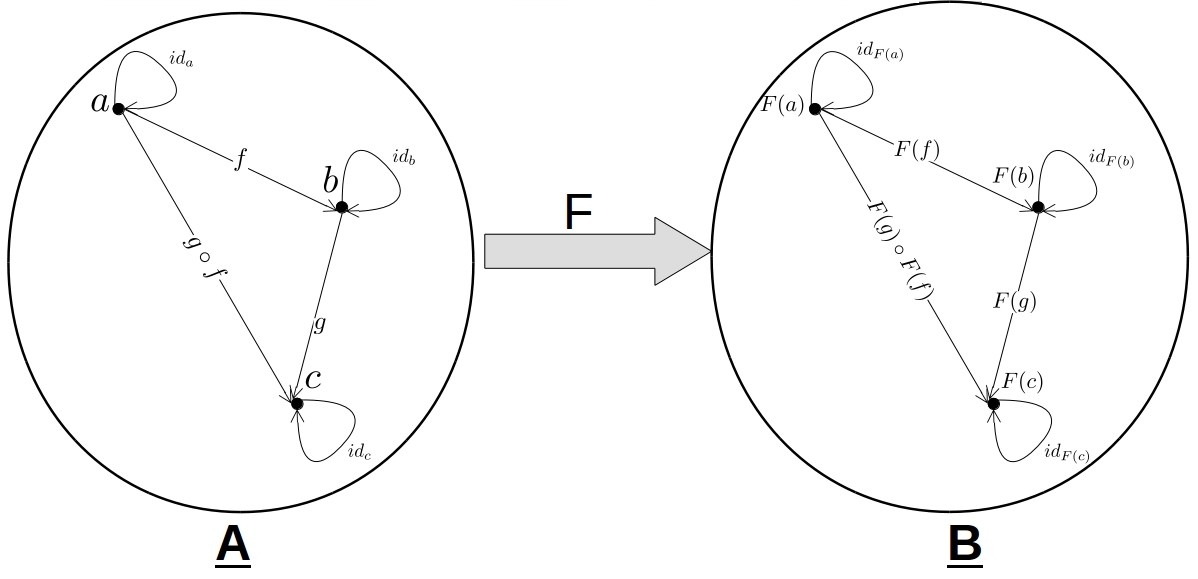
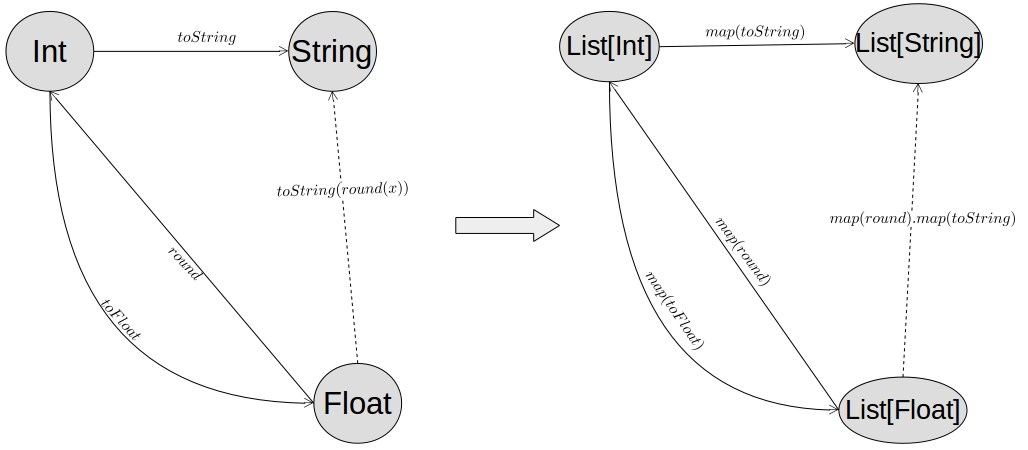
在Catetory Theory中，一个Functor F是两个范畴A和B之间的变换，我们写成F : A → B，F必须将A的每一个对象和箭头映射到B，换句话说，如果a∈ob(A)，那么F(a)∈ob(B)，如果f∈Hom(A)，那么F(f)∈Hom(B)。另外F还需要保留A的结构(比如箭头和箭头间的组合)，也就是说：

如果f : a → b是A中的一个箭头，那么F(f) : F(a) → F(B)是B中的一个箭头
F(idX) = id(F(X))，即A中的每个identity箭头都转化为B中相应对象的identity箭头
F(g ∘ f) = F(g) ∘ F(f)，即A中的箭头组合的映射是箭头在B中的映射的组合

简单来说，就是：

当然，functor也可以将一个Category A转化为自身，这时的functor是endofunctor，写成F : A → A。

函数式编程中的Functor

来看看熟悉的代码，对应之前的Functor的定义，在Haskell中它是这样定义的：

1
2


class Functor f where
    fmap :: (a -> b) -> f a -> f b

fmap 就是实现两个Category转换的关键，(a -> b)是A里的一个箭头，变成了B里的一个箭头f a -> f b，这就是它要做的事。

在Category中Functor需要一些条件，在编程中也对应着一些laws，比如Functor的laws:

1
2


fmap id = id
fmap (g . f) = fmap g . fmap f

如果我们的实现满足这些laws，就是一个合法的Functor。

List Functor

最常见的Functor应该就是List了，我们在日常写代码过程中经常用到：

对于List，我们应该怎么实现 fmap呢？太显然了，就是我们整天用的map。

1
2


instance Functor [] where
    fmap = map

平时写代码的时候可能都没意识到自己在用Functor，比如很自然就会写出

1

[1, 2, 3, 4].map(x => x.toString()) // ["1", "2", "3", "4"]

1

Enum.map([1, 2, 3, 4], &to_string/1) # ["1", "2", "3", "4"]

我们其实是将一个Category Int中的对象映射到了Category String中的对象。

Maybe Functor

另一个十分重要的Funtor就是Maybe，我们先来看看什么是Maybe，它在Haskell中定义如下：

1

data Maybe a = Just a | Nothing

也就是说Maybe的值有两种可能：Just a或者Nothing，这有什么用？

比如我们要定义一个开根号的方法，我们一般会这样做：

1
2


sqrt x | x >= 0 = Just $ ... -- ...代表具体的开根号实现
       | otherwise = error "The value must be larger or equal to 0"

我们可以在x < 0的时候抛出异常，如果不影响后边的运算则catch这个异常继续运算，我们的代码里会有很多判断error的地方，这非常不函数式。

Maybe可以帮我们解决这个问题，我们可以将sqrt定义成这样：

1
2


sqrt x | x >= 0 = Just $ ...
       | otherwise = Nothing

这里sqrt返回一个Maybe类型的值(Just x | Nothing)，这样我们可以将Maybe 值继续向后传给接受Maybe类型参数的函数。

假设我们有一个Int值：3，我们很容易就可以对它进行运算，比如把它传给(+2)这个函数，我们就会得到 5。

那我们怎么能给一个Maybe值实现加2呢？(+2) Just(3)会报错的，答案就是Functor。

(+2)这个函数的类型是 Int -> Int (其实是Num a => a -> a，这里我们为了方便将其指定为Int)，而我们想要的是Maybe Int -> Maybe Int，这正好是Functor可以帮我们做到的，这时Functor实现的就是：

1

(Int -> Int) -> Maybe Int -> Maybe Int

下面是Maybe的Functor实现：

1
2
3


instance Functor Maybe where
    fmap f Nothing  = Nothing
    fmap f (Just x) = Just (f x)

这时我们就可以：

1
2


fmap (+2) Nothing -- Nothing
fmap (+2) Just(3) -- Just(5)

举这种十分简单的例子有一个弊病，就是其作用不明显，我们找一个稍微复杂一点点的例子。比如我们要通过id从数据库读取Post记录，然后得到其title字段，我们可以这样实现：

1
2
3
4
5
6


post = Post.find_by_id(1)
if post
  return post.title
else
  return nil
end

有了Maybe Functor，我们可以用更优雅的方式：

1
2


fmap (getPostTitle) (findPost 1)
-- 等价于 getPostTitle <$> (findPost 1)

Conclusion

Category Theory和函数式编程的关系十分紧密，Functor可以帮我们建立一个最初的印象，之后就可以继续学习Applicative, Monad, Traversable等概念了。