函数式编程基础--Monoid, Foldable and Traversable

Monoid(幺半群)

Monoid是一个数学上的概念：

幺半群是一个存在单位元（幺元）的半群

即，考虑定义了二元运算 ∘ : S -> S（注意这里蕴含了S对运算∘ : S -> S封闭）的非空集合S，若满足如下公理：

结合律：∀ a, b, c∈ S，有 (a∘b)∘c = a∘(b∘c)

单位元：∃ e∈S ，使∀ a∈ S，有 a∘e = e∘a

则三元组<S, ∘, e>称为幺半群。

看到结合律有没有勾起童年的回忆？就是小学数学的加法结合律：

1
2


(5 + 6) + 10 -- 21
5 + (6 + 10) -- 21

有了结合律，还需要一个幺元，所有数和它进行运算(相加)都等于自身，很明显就是0。

1
2


255 + 0 -- 255
0 + 255 -- 255

当然乘法也有结合律，这时幺元就是1了。

不止数值，还有很多其他的类型也可以满足这些条件，比如List和String：

1
2
3
4


([1,2,3] ++ [4,5,6]) ++ [7,8,9] -- [1,2,3,4,5,6,7,8,9]
[1,2,3] ++ ([4,5,6] ++ [7,8,9]) -- [1,2,3,4,5,6,7,8,9]
[1,2,3] ++ []                   -- [1,2,3]
[] ++ [1,2,3]                   -- [1,2,3]

在编程领域中，Monoid是这样定义的：

1
2
3
4
5
6


class Monoid a where
    mempty  :: a
    mappend :: a -> a -> a

    mconcat :: [a] -> a
    mconcat = foldr mappend mempty

我们可以把mempty当作幺元，把mappend当作那个二元运算。mconcat就是遍历一个List然后把其中的元素用mappend连起来最后组成单个元素(第一个元素和幺元进行运算)：

1

mconcat ["Tree", "fingers"] -- "Treefingers"

还有我们经常用的reduce函数本质上就是做了这个：

Elixir

1
2
3


Enum.reduce [1, 2, 3], &+/2 # 6
# 等价于
Enum.reduce [1, 2, 3], 0, fn x, acc -> x + acc end

Javascript

1
2
3
4


const array = [1, 2, 3]
const reducer = (accumulator, currentValue) => accumulator + currentValue
// 1 + 2 + 3
console.log(array.reduce(reducer))

完整性起见，这里把Monoid需要满足的laws写在这，其实就是对应了数学定义：

1
2
3


(x <> y) <> z = x <> (y <> z) -- associativity
mempty <> x   = x             -- left identity
x <> mempty   = x             -- right identity

Foldable

在上边的Monoid中，我们看到了mconcat的实现，它用了foldr这个函数，foldr是个很有用的函数，被用在很多地方，它的类型是这样的:

1

foldr :: (a -> b -> b) -> b -> [a] -> b

首先我们要提供一个函数f :: (a -> b -> b)，然后给一个初始的b和一个 [a](List a)，foldr会遍历[a]并利用函数f最终生成一个b（注意这里的a，b是类型变量）。

有了foldr就可以实现Foldable，Foldable的定义如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


-- Abridged definition, with just the method signatures.
class Foldable t where
    foldMap :: Monoid m => (a -> m) -> t a -> m
    foldr :: (a -> b -> b) -> b -> t a -> b

    -- All of the following have default implementations:
    fold :: Monoid m => t m -> m -- generalised mconcat
    foldr' :: (a -> b -> b) -> b -> t a -> b
    foldl :: (b -> a -> b) -> b -> t a -> b
    foldl' :: (b -> a -> b) -> b -> t a -> b
    foldr1 :: (a -> a -> a) -> t a -> a
    foldl1 :: (a -> a -> a) -> t a -> a
    toList :: t a -> [a]
    null :: t a -> Bool
    length :: t a -> Int
    elem :: Eq a => a -> t a -> Bool
    maximum :: Ord a => t a -> a
    minimum :: Ord a => t a -> a
    sum :: Num a => t a -> a
    product :: Num a => t a -> a

Foldable的函数有很多，但是在实现的时候只需要实现flodMap或者foldr其中一个就可以了，其他的函数都可以用这两个函数间接实现。

Foldable和Functor都是遍历List，回顾一下Functor：

1
2
3


instance Functor [] where
    fmap _ []     = []
    fmap f (x:xs) = f x : fmap f xs

fmap f遍历一遍列表，将f应用到每个元素上，生成一个新的列表。类似地，foldMap f也遍历列表，将f应用于每个元素，不同之处是flodMap会利用mappend将结果组合起来。然而有一种遍历是fmap和flodMap都无法做到的，设想我们有这样一个函数：

1
2


deleteIfNegative :: (Num a, Ord a) => a -> Maybe a
deleteIfNegative x = if x < 0 then Nothing else Just x

deleteIfNegative接收一个数值，如果是负数则返回Nothing，如果不是负数则返回Just x ，也就是说deleteIfNegative的返回值是一个Maybe 类型。

然后我们想利用它实现下边的函数：

1

rejectWithNegatives :: (Num a, Ord a) => [a] -> Maybe [a]

rejectWithNegatives接收一个[a]，如果List里有负数则返回Nothing，如果都不是负数则返回Just [a]，这时候如果使用fmap：

1
2
3


GHCi> let testList = [-5,3,2,-1,0]
GHCi> fmap deleteIfNegative testList
[Nothing,Just 3,Just 2,Nothing,Just 0]

不太行，正如之前所说，fmap就是把f作用列表上，返回的是[Maybe a]；而flodMap也不行，虽然它会把经过f处理过的元素组合起来，这时我们需要的是Traversable。

Traversable

先来看一下定义：

1
2
3
4
5
6
7
8


class (Functor t, Foldable t) => Traversable t where
    traverse  :: Applicative f => (a -> f b) -> t a -> f (t b)
    sequenceA :: Applicative f => t (f a) -> f (t a)

    -- These methods have default definitions.
    -- They are merely specialised versions of the other two.
    mapM      :: Monad m => (a -> m b) -> t a -> m (t b)
    sequence  :: Monad m => t (m a) -> m (t a)

traverse和sequenceA也可以互相实现，所以我们只需要实现一个就可以，剩下的函数都可以用这两个函数定义出来：

1
2


traverse f = sequenceA . fmap f
sequenceA  = traverse id

来看看用Traversable怎么解决实现rejectWithNegatives的问题，首先我们要对List实现Traversable:

1
2
3
4
5
6
7
8


instance Traversable [] where
    -- sequenceA :: Applicative f => [f a] -> f [a]
    sequenceA []     = pure []
    sequenceA (u:us) = (:) <$> u <*> sequenceA us

-- 等同于:
instance Traversable [] where
    sequenceA us = foldr (\u v -> (:) <$> u <*> v) (pure []) us

有了Traversable，我们就可以实现rejectWithNegatives了：

1
2
3
4
5
6
7


GHCi> let rejectWithNegatives = sequenceA . fmap deleteIfNegative
GHCi> :t rejectWithNegatives 
rejectWithNegatives :: (Num a, Ord a, Traversable t) => t a -> Maybe (t a)
GHCi> rejectWithNegatives testList
Nothing
GHCi> rejectWithNegatives [0..10]
Just [0,1,2,3,4,5,6,7,8,9,10]

当然我们可以用traverse函数来实现：

1
2


rejectWithNegatives :: (Num a, Ord a, Traversable t) => t a -> Maybe (t a)
rejectWithNegatives = traverse deleteIfNegative

traverse的类型是 (a -> f b) -> t a -> f (t b)，而deleteIfNegative的类型是a -> Maybe a，所以traverse deleteIfNegative 的类型正好是 t a -> Maybe (t a)。

照例写一下Traversable的laws：

1
2
3
4


-- identity law
traverse Identity = Identity
-- composition law
traverse (Compose . fmap g . f) = Compose . fmap (traverse g) . traverse f

有了Traversable之后，List的遍历操作就相对完整了。

我们再来看一下traverse做了什么：

1

traverse :: (Traversable t, Applicative f) => (a -> f b) -> t a -> f (t b)

单看这个类型，可以感觉出来它和fmap :: (a -> b) -> f a -> f b冥冥中貌似有些联系，其实我们是可以用traverse来实现fmap的，traverse比fmap多了些东西，也就是f，如果我们能把traverse中的f去掉就会得到一个fmap了：(a -> b) -> t a -> t b。而这里的f是一个Applicative，我们需要找到一个Applicative达到“去掉自己”的目的，去掉自己其实就是说这个Applicative没有任何操作，只是为了达到Applicative要求的一个容器，而这正是Identity做的事：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


newtype Identity a = Identity { runIdentity :: a }

instance Functor Identity where
      fmap f (Identity x) = Identity (f x)

instance Applicative Identity where
      pure = Identity
      Identity f <*> Identity x = Identity (f x)

instance Monad Identity where
      return = pure
      Identity x >>= f = f x

Identity我们可以理解成一个只有Just的Maybe类型，什么都不做，就是封装一下数据，想拿出来就拿出来，我们可以利用它实现traverse到fmap的转换：

1
2


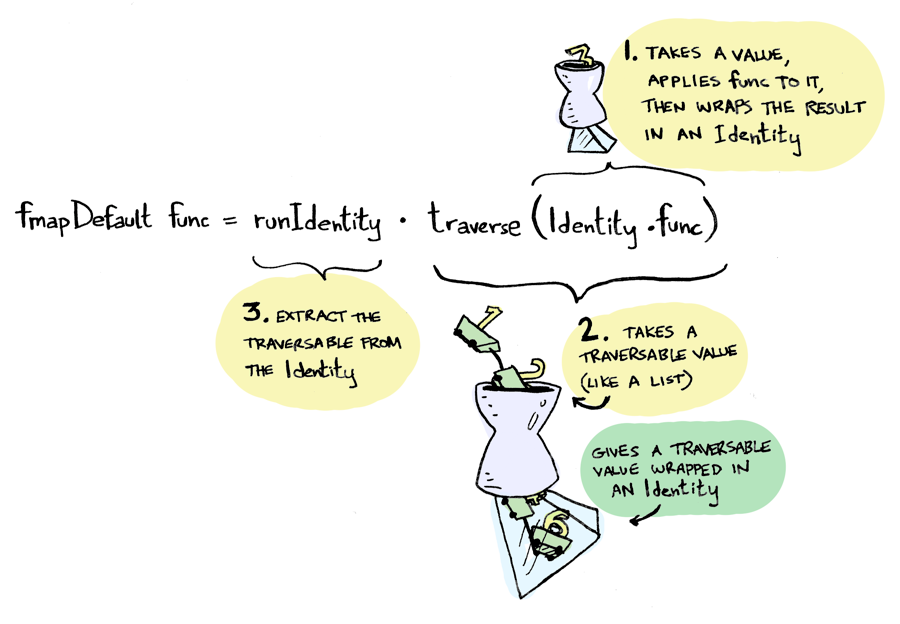
fmapDefault :: Traversable t => (a -> b) -> t a -> t b
fmapDefault f = runIdentity . traverse (Identity . f)

它的工作原理是这样的：

如果我们一步一步地看各个步骤的类型，就会是这样的：

1
2
3
4
5


-- f :: a -> b
-- Identity . f :: a -> Identity b 
-- traverse :: (a -> Identity b) -> t a -> Identity (t b)
-- traverse (Identity . f) :: t a -> Identity (t b)
-- runIdentity . traverse (Identity . f) :: t a -> t b

Conclusion

到此为止我们已经熟悉了Functor, Applicative, Monad, Foldable和Traversable这五种type classes，有了这些武器就可以继续了解更多函数式编程中的概念了。上边那个traverse转换成fmap的过程是很有趣的，它正是理解lens的基础，关于lens我们在之后的文章再分解。

文章目录