LambdaCalculus

函数

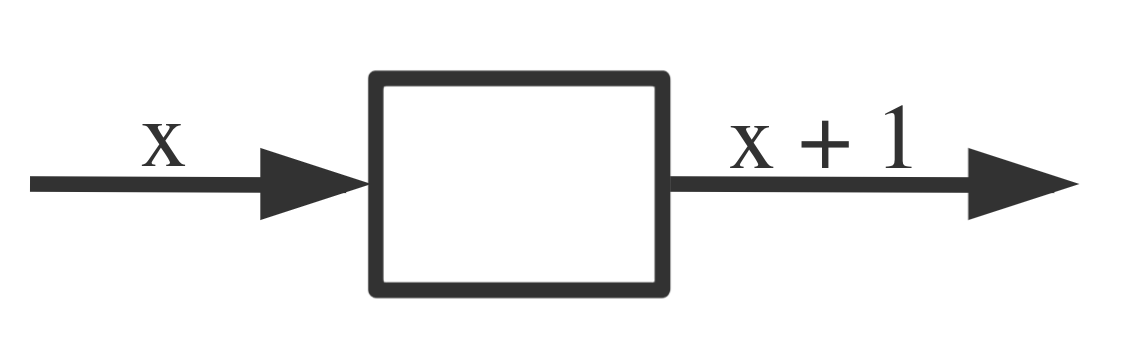
我们先从函数开始，在这里我们将函数看成一个黑盒，你不能看到里边是什么，它需要一些输入，以某种方式处理它，然后产生一个输出。举个简单的例子，下边这个函数只接受一个输入x，输出x+1：

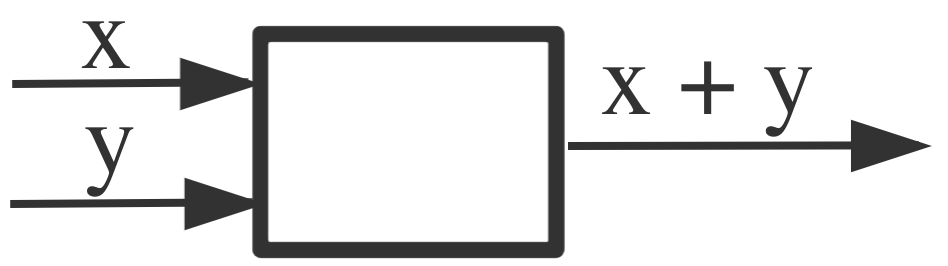
This is sample image

我们也可以有另一个一个黑盒，它有两个输入x和y，以某种方式处理它们然后输出x + y。

This is sample image

在这个意义上，关于函数有两个重要的东西：

  • 第一个就是那个黑盒，你不知道盒子里发生了什么，你能做的就是把一些东西放进去，然后观察从另一边出来的是什么。
  • 第二个是这些函数是纯函数，它们没有内部状态。所以当你把x映射到x+1上时，盒子里的处理过程就发生了，没有内部状态，没有我们可以利用的隐藏信息，这与我们熟悉的图灵机的计算概念有很大的不同。

在λ 演算中我们可以用很简单的语法来定义函数，比如上边的x + 1函数，他的定义方法就是先用一个λ 符号代表引入了一个函数，然后写下输入的名字x。然后用一个点表示输出是如何根据输入来计算的，即x+1： $$ λ x.x+1 $$ 相加函数也是一样，它有两个输入x和y，然后给出结果x+y，我们可以写成这个形式: $$ λx.λy.x+y $$ 当你有一个函数时，你能用它做什么？你所能做的就是给它一些输入，然后让它给你一些输出。举个简单的例子，如果我们把$\lambda x.x+1$应用到一个数上，比如10，会发生什么？ $$ (λ x.x+1) 10 $$ 这其实就是一个基本的替换过程，我们本质上是把这里的数字10代入到这个表达式中然后x变成10，然后这个函数会运算10+1，然后我们得到结果11，这就是λ 演算的基本内容，它只有三个东西:

  • 变量x, y, z…
  • 如何构造一个函数λ
  • 如何应用函数λ

编码

函数看起来很简单，甚至好像没什么用，其实它的地位还是很重要的，有很多应用，我们举几个例子：

  1. λ演算可以对任何计算进行编码。如果你用任何顺序编程语言(sequential programming language)写程序，它都可以以某种方式编码在λ演算中。当然它可能是非常低效的，但这不是重点，这是计算的一个基本概念。我们感兴趣的是我们可以在其中编码什么样的程序，实际上你可以对任何东西进行编码，任何图灵机程序都可以翻译成等价的λ演算程序，反之亦然。

  2. λ演算也可以被看作是函数式编程语言的基础，比如Haskell，它实际上是一种非常复杂的语言，但是可以被编译成一个非常小的核心语言，本质上就是λ演算的作用。

  3. λ演算实际上现在存在于大多数主要编程语言中，像Java, C#和F#等等这些语言，现在都将Lambda演算作为基本组件。

我们举几个例子来说明如何使用它，λ演算很简单，就是上边提到的三个组成部分：变量，构造函数的方法和应用函数的方法。它没有任何内建的数据类型，如数字，逻辑值，递归等等。如果你想用这些东西，你需要对它们进行编码。

编码Bool运算

这里先展示一个简单的编码，就是逻辑值TRUE和FALSE，关键是要思考，在编程语言中，如何处理逻辑值的，我们用它们在两件事之间做出选择，如果某个条件是真的，做一件事，如果条件是假的，做另一件事。我们就要用这个在两个东西之间做出选择的概念来编码真和假，具体的编码如下: $$ TRUE = λx.λy.x $$

$$ FALSE = λx.λy.y $$

对于TRUE，它需要x和y两个变量，然后它会给你返回第一个，而FALSE则做了相反的事情。

我们能利用它做些什么呢？我们来想一下如何用它来定义NOT运算符，这很容易做到，我们输入一个布尔值b，然后把FALSE和TRUE两个参数应用在b上。 $$ NOT = \lambda b.b \hspace{3mm} FALSE \hspace{3mm} TRUE $$ 我们来检查一下，如果我们将NOT应用在TRUE上会发生什么，我们唯一能做的就是展开定义： $$ NOT \hspace{3mm} TRUE = (\lambda b.b \hspace{3mm} FALSE \hspace{3mm} TRUE) \hspace{3mm} TRUE = TRUE \hspace{3mm} FALSE \hspace{3mm} TRUE $$ 现在我们要做的是展开TRUE的定义，TRUE接收两个东西，然后选择第一个，所以我们得到一个函数$(\lambda x. \lambda y.x)\hspace{3mm} FALSE \hspace{3mm} TRUE$，它有两个参数，选择第一个参数，第一个参数是FALSE，当我们应用这个函数时，我们得到的就是FALSE。

通过这种方式你可以很容易地检验NOT FALSE，我们也可以编码 AND和OR: $$ AND = λx. λy. x \hspace{3mm} y \hspace{3mm} FALSE $$

$$ OR = λx. λy. x \hspace{3mm} TRUE \hspace{3mm} y $$

有兴趣的话可以自己验证一下，作为练习，你可以考虑一下如何编码 XOR！

编码递归

如果我们想对递归进行编码怎么办呢？这就要用到非常著名的Y组合子(Y Combinator)： $$ Y = λf.(λx.f(x \hspace{3mm} x))(λx.f(x \hspace{3mm} x)) $$ Y组合子就长成上边这个样子，它是不动点组合子之一，也是在λ演算中对递归进行编码的关键。它是由一个叫Haskell Curry的人发现的(没错，Haskell语言的名字就是从他这来的)，我们来看一下这个Y组合子是怎么编码递归的。

递归就是用事物本身来定义事物，一个简单的例子就是阶乘函数，想想我们是如何定义阶乘函数的，如果用递归的话，我们有一个很简单很自然的定义，你给阶乘函数一个数字n，它会在做两件事之间做出选择：如果数字等于1，返回结果1；否则，它会用这个数乘以它前一个数的阶乘。这是一个递归函数，因为我们用它本身来定义阶乘，任意数n的阶乘是由n-1的阶乘定义的，这就是递归的工作方式。

我们先简化一下这个问题，从最简单的递归开始，我能想到的最简单的递归定义就是一个循环的程序，它什么都不做，就是一直循环，也就是:

1

LOOP = LOOP

如果你运行上边这个东西，它会原地打转，什么都不做，这是一个最简单的递归程序。那么如何在λ演算中编码这个行为呢？这里的关键是self application，就是把一个东西应用到它自己，在这个例子中就是把一个函数应用到它自己，我们可以这样对循环进行编码: $$ LOOP = (λx.x \hspace{3mm} x)(λx.x \hspace{3mm} x) $$ 这里有两个函数（其实是同一个函数的两个拷贝），可以理解成把一个函数应用到了它自身，这就是self application。这种思想也发生在函数的具体作用层面上，这个函数接收一个叫做x的输入，然后将x应用于自身，再一次应用了self application。这个思想是·在一种不支持循环和递归的语言中进行循环或递归的关键。

接下来我们来看一下这个东西是否真的执行了循环，回顾一下函数的实际作用，它接受一个输入，然后它会告诉你怎么处理这个输入。在这个例子中，输入就是$(\lambda x.x \hspace{3mm} x)$，它被应用在$(\lambda x.x \hspace{3mm} x)$上，返回的结果就是$(λx.x \hspace{3mm} x)(λx.x \hspace{3mm} x)$。

这就是循环的定义，我们得到了完全一样的结果。如果我们再做同样的事，我们还会得到完全相同的结果，我们编码了循环的概念！这是一个简单的例子我们来看一个更一般的递归例子，先看看递归的定义，我要定义一个叫做reck的递归函数：

1
2

rec f = f (rec f)
      = f(f(f(f(...))))

它会接受另一个函数f作为输入，接下来要做的就是把这个函数应用到f上，这就是计算机科学中所谓的一般递归的概念。这是最常见的递归模式，任何其他递归函数都可以用这个来编码，所以如果我们可以在λ演算中编码rec，我们就可以对任何递归函数进行编码。比如 我们可以用rec来编码loop：loop = rec(λx.x)，你可以思考一下如何定义阶乘函数。

如果我们能编码rec，然后我们就可以编码递归了，我们再看一下上边的Y组合子： $$ Y = λf.(λx.f(x \hspace{3mm} x))(λx.f(x \hspace{3mm} x)) $$ 你看这一堆符号它实际上和LOOP非常相似，忘了的话可以回头看看LOOP的定义，它有self application的想法，即将一个函数应用在自身上。这就是Y组合子，它不是递归，但它编码递归。这是一个非常简单但强大的想法，你可以在大多数编程语言中这样做(除非这个语言有某种类型系统阻止你这么做)，这就给本来没有递归的语言赋予了递归的能力。那Y组合子到底是怎么编码rec这个函数的呢？其实只要展开它就可以了，我们可以用一个例子函数g来展开它。

1
2
3
4
5
6

(Y g)
= (λf.(λx.(f (x x)) λx.(f (x x))) g)
= (λx.(g (x x)) λx.(g (x x)))
= (λy.(g (y y)) λx.(g (x x)))           ---- (1)
= (g (λx.(g (x x)) λx.(g (x x))))
= (g (Y g))

在(1)处我们用α转换重命名了约束变量，这是没问题的，可以让我们看的更清楚，至此我们就编码了rec函数，即递归。

关于λ 演算的应用的介绍到这里就结束了，希望对你有所帮助。